 As a Ph.D. candidate, my research focused on the development of an efficient computational algorithm suitable for simulations of electrical impulses in nerve cells. Current research in computational neuroscience involves simulations of electrical impulses that travel through large computational domains, such as the example shown to the left from the Blue Brain Project. In many cases there is a spatial localization of activity, with a small region of the cell (or network of cells) changing rapidly while the majority of the system evolves very little. By taking advantage of this spatial localization of activity, I was able to develop an algorithm that can be more efficient than the standard approach. In a traditional simulation algorithm, the entire cell is treated as a single large system that is solved simultaneously. Thus in order to obtain an accurate solution, the entire system must be updated using a time step size that is sufficiently small to capture the fastest evolution, even though most of the system could be accurately updated using a much larger time step.
As a Ph.D. candidate, my research focused on the development of an efficient computational algorithm suitable for simulations of electrical impulses in nerve cells. Current research in computational neuroscience involves simulations of electrical impulses that travel through large computational domains, such as the example shown to the left from the Blue Brain Project. In many cases there is a spatial localization of activity, with a small region of the cell (or network of cells) changing rapidly while the majority of the system evolves very little. By taking advantage of this spatial localization of activity, I was able to develop an algorithm that can be more efficient than the standard approach. In a traditional simulation algorithm, the entire cell is treated as a single large system that is solved simultaneously. Thus in order to obtain an accurate solution, the entire system must be updated using a time step size that is sufficiently small to capture the fastest evolution, even though most of the system could be accurately updated using a much larger time step.
To take advantage of the spatial localization of activity, I developed an algorithm for locally adaptive time stepping (LATS). Within this scheme, the system is split into subdomains, and each subdomain is updated with an adaptive time step most appropriate for the local level of activity, as shown in the figure below. The challenge of localized adaptive time stepping is in maintaining accurate flow of information and stability of the solution. Through the application of domain decomposition techniques, I was able to computationally connect the subdomains through boundary conditions obtained through a conservation of flux. To address the stability concerns, I replaced the time stepping scheme that had been used for neuroscience simulations since the 1960’s with a method that provides better stability and proved better suited to the LATS algorithm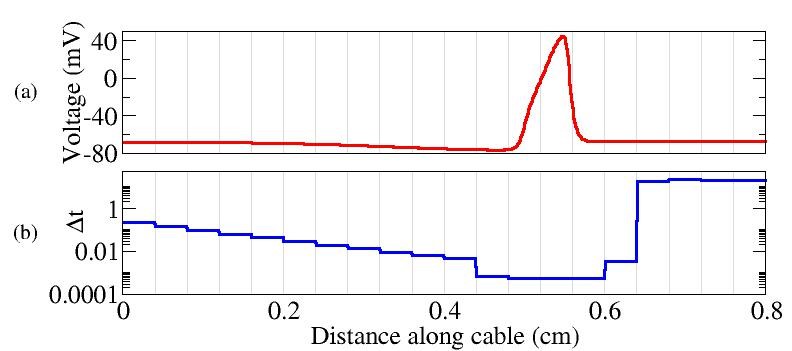 .
.
Evaluating the LATS algorithm is not as simple as stating an X% reduction in computational time. The underlying numerical scheme is comparable to the standard approach, but the major benefit of the LATS method is that the computational cost scales with the level of activity in the system, rather than the physical size of the domain. Thus in situations where there is sparse activity in a large computational domain, the LATS method provides a significant reduction in computational cost by focusing computational resources where they are most needed. The LATS method was developed within the context of computational neuroscience, but is applicable to any system with sparse activity.
In the video below, an electrical impulse is initiated in a cell, and propagates through two cells. The colors represent the membrane voltage, and the sections of the cell become transparent as the step size increases.
For more details, read the full paper here.
Do you have an application where the LATS methods could be helpful? I’d like to discuss it.
