As an M.Sc. student, I worked on a model describing the early stages of
type 1 diabetes. Type 1 diabetes occurs when the immune system attacks and destroys the insulin producing beta-cells in the pancreas. Our
experimental collaborator had observed that macrophages (a part of the immune system that clears away dead cells from tissues) from mice susceptible to type 1 diabetes were less efficient than macrophages from healthy mice. It was also observed that not every mouse susceptible to the disease developed it. Based on these observations, we developed a model to answer two questions:
1. Can the difference in macrophage efficiency account for the differences observed between healthy and susceptible mice?
2. Can a naturally occurring wave of beta-cell death associated with normal development in all mice be a triggering event that leads to type 1 diabetes in susceptible mice?
Within our modeling framework, the healthy state corresponds to a steady-state solution representing no inflammation, while the diseased state corresponds to a steady-state solution representing chronic inflammation. It is then assumed that during the chronic inflammation state the immune system will become primed to attack and kill the pancreatic beta-cells. Since not all susceptible mice develop type 1 diabetes, the healthy state should exist and be stable for both strains of mice being modeled. In addition, the steady state corresponding to chronic inflammation should exist and be stable for the susceptible mice. Through the use of dynamical systems approaches (especially phase-plane analysis) we determined that the initial model could not satisfy these requirements for biologically reasonable parameter values. The model was then expanded to include additional cell populations as well as the toxic effect of harmful cytokines released by the macrophages. This expanded model, shown below, demonstrated that differences in macrophage efficiency could explain the difference between healthy and susceptible mice.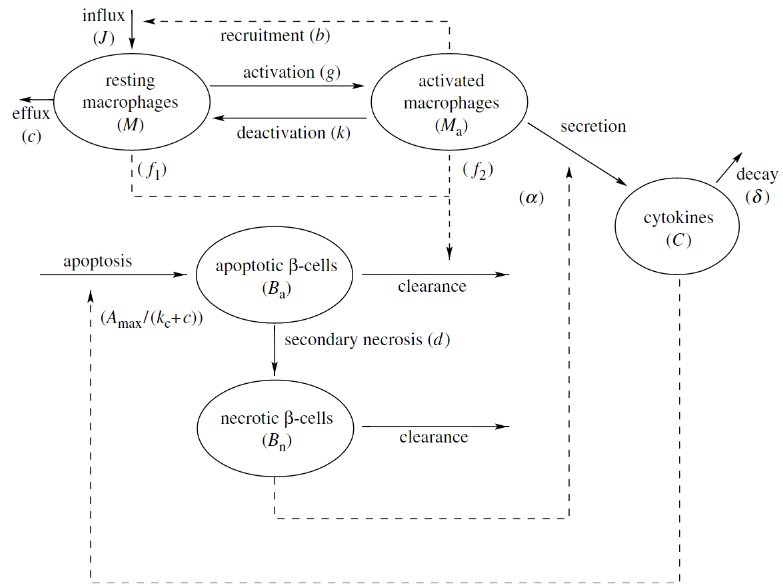
To answer the second question, the wave of beta-cell death was incorporated into the model. The model demonstrated that for healthy mice the temporary inflammation quickly died down, and the model returned to the non-inflamed steady state. In the case of the susceptible mice, the wave of beta-cell death was sufficient to push the system to chronic inflammation, suggesting that the naturally occurring cell death could indeed be a triggering stimulus for the development of type 1 diabetes.
For more details, read the full paper here.

 As a Ph.D. candidate, my research focused on the development of an efficient computational algorithm suitable for simulations of electrical impulses in nerve cells. Current research in computational neuroscience involves simulations of electrical impulses that travel through large computational domains, such as the example shown to the left from the
As a Ph.D. candidate, my research focused on the development of an efficient computational algorithm suitable for simulations of electrical impulses in nerve cells. Current research in computational neuroscience involves simulations of electrical impulses that travel through large computational domains, such as the example shown to the left from the 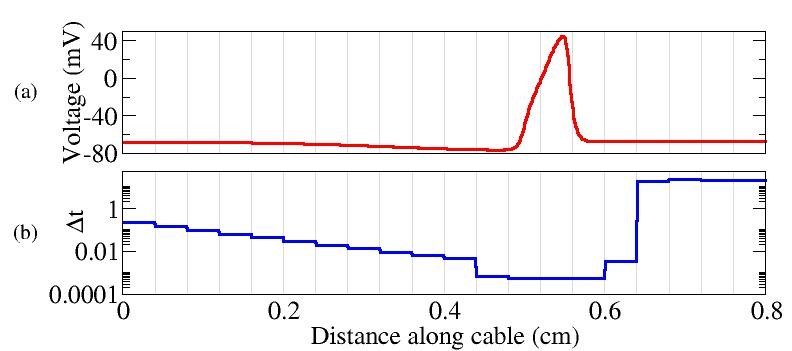 .
.