
After working as a software developer for a few years, I’m ready for something different. I’ve explored a few different options and have decided to pursue a career in data science.
How will I make this switch? Following the advice of Marc Miller, I’ve talked to a number of people to find out what a data scientist does, the skills needed, and how to get a data science job.
The term data scientist is not well defined and means different things to different people (Chad Bryant has an excellent summary here), but common advice is to create a portfolio to demonstrate what you can do. Ideally this will contain a variety of projects showcasing your expertise. I’m currently working towards developing this portfolio.

Step 1 is to gain some basic skills, and I’ve decided to begin by working through the many courses at DataCamp. DataCamp offers courses in Python and R (the main two languages used for data science), and since I already am proficient in Python, I’m tackling the R courses. I’m hoping that through these courses I’ll gain an overview of the basic concepts, and will have the tools to begin building my portfolio.
Step 2 in my plan is to work through more in depth courses. I haven’t decided what provider to use yet, but there seem to be many options (through udacity, edX, udemy, etc.). These courses dig deeper into the material, and also provide projects that can be included in a portfolio.
Step 3 is to go it alone: find a data set and see what I can do. This step could also include Kaggle competitions as these tend to have nicer data sets and clearly defined questions that could make a first project more manageable.
Through all of this I’m continuing to meet people and learning about what they do. Do you work as a data scientist? I’d love the opportunity to talk to you.

 As a Ph.D. candidate, my research focused on the development of an efficient computational algorithm suitable for simulations of electrical impulses in nerve cells. Current research in computational neuroscience involves simulations of electrical impulses that travel through large computational domains, such as the example shown to the left from the
As a Ph.D. candidate, my research focused on the development of an efficient computational algorithm suitable for simulations of electrical impulses in nerve cells. Current research in computational neuroscience involves simulations of electrical impulses that travel through large computational domains, such as the example shown to the left from the 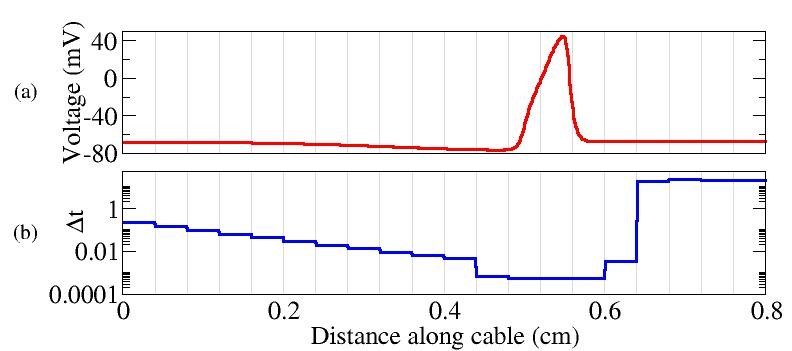 .
.